how to find center and radius of a circle

Completing the Square: Circle Equations

The technique of completing the foursquare is used to turn a quadratic expression into the sum of a squared binomial and a number.

In other words, completing the square volition catechumen a generic quadratic into something along the lines of this:

(x − s)² + t

Content Continues Below

The center-radius grade of the circumvolve equation is in this format:

(x − h)² + (y − m)² = r ²

What is the reward of the completed-square, center-radius grade of a circle's equation?

In completed-square form, the eye of the circle is shown every bit existence at the point (h, k) and the radius is shown as existence " r ". This form of the equation is helpful, because it allows you to hands read off the coordinantes of the heart and the length of the radius.

Just circle equations are often given in the general format forth the lines of:

x ² + y ^two + dx + ey + f = 0

When you are given this general form of equation and told to discover the eye and radius of a circle, yous volition have to consummate the foursquare to catechumen the equation to heart-radius form. This lesson explains how to make that conversion.

What is an example of completing the square to find a circumvolve'due south center and radius?

• Notice the center and radius of the circle having the following equation: ivx ² + foury ^two − sixteenx − 24y + 51 = 0.

Here is the equation they've given me:

ivx ² + 4y ⁱⁱ − xvix − 24y + 51 = 0

Offset, I'll move the loose number over to the other side of the "equals" sign:

4x ² + 4y ² − xvix − 24y = −51

Now I'll grouping the x -stuff together, and the y -stuff together:

410 ² − 16x + 4y ² − 24y = −51

Whatever is multiplied on the squared terms (it'll ever be the same number), I'll divide information technology off from every term on each side of the "equals" sign:

Now comes the complicated footstep. I'll need to insert extra space inside my groupings, because this is where I'll add the squaring term.

To make full in the first parenthetical, I take the ten -term coefficient (that is, the number multiplied on the linear x , not the squared x ⁱⁱ term), multiply it by ane-half, square the result, and then add this squared value to both sides of the equation. In this case, the number is −4; half of this is −2; the square of this is +4. So I add a +4 inside the x parenthetical, and I also add this to the other side of the equation:

Now I'll practice the same with the y -term coefficient: I'll take half of the coefficient, square it, and add the result to each side of the equation. In this instance, the coefficient is −half dozen, so half of that is −3, and the square is +9, which I'll add together to both sides of the equation:

The values that I got by multiplying by 1-one-half (or, which is the same thing, past dividing in half) are the values for completing the ii squares on the left-hand side of my equation:

On the right-hand side of the equation, I need to simplify:

The numerical value on the correct-hand side is the square of the length of the radius. In this instance, the value is ¼, which is the square of ½:

I've completed the ii squares and have found the square of the radius. From this heart-radius class of the equation, I can hands read off the solution:

center: (h, k) = (2, 3)

radius:

---

Yous can trace the logic in the paradigm below:

---

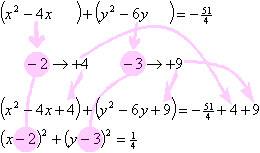
What are the steps for completing the foursquare for a circle equation?

1. If anything is multiplied on the squared terms (and it'll be the same value on each of the squared-variable terms), so divide through on both sides of the equation by that value.
2. Collect the x -containing terms together, and collect the y -containing terms together.
3. Motion whatsoever stand-alone numbers to the other side of the "equals" sign.
4. Rewrite the equation, from the previous line, with parentheses effectually the grouped x and y terms, leaving extra space for a 3rd value to exist added in.
5. Detect half of the coefficients of each of the linear x and y terms (not the squared terms!).
6. Square each of these new values.
7. Take these squares and ddd (on the left-manus side) within the advisable ready of parentheses; add together (on the correct-hand side) to whatever existing numerical value(s).
8. Convert the parentheticals on the left-hand side to completed-square class by replacing the quadratic with the variable and the value you constitute for that variable in Pace 5 above. Remember to put a superscripted ii on each set of parentheses.
9. Convert the numerical expression on the right-paw side to radius form by simplifying
10. Notice the value of the radius by taking the square root of this simplified value.

---

Completing the foursquare to find a circle's heart and radius always works in this fashion. Always do the steps in this club, and each of your exercises should work out fine. (Also, if you get in the habit of e'er working the exercises in the same manner, you are more likely to call back the procedure on tests.)

Alarm: Don't misinterpret the last equation. Recollect that the circle formula is:

(x − h)² + (y − chiliad)ⁱⁱ = r ²

If you end up with an equation like this:

(x + iv)² + (y + 5)² = 5

...you have to keep straight that h and k are subtracted in the eye-radius grade, so you lot actually accept this equation:

(x − (−four))ⁱⁱ + (y − (−5))² = 5

That is, the centre, based on the equation to a higher place, is at the betoken (−4, −5), not at (iv, 5). Be conscientious with those signs; don't just "read off the reply" without thinking.

Also, remember that the formula says " r ² ", not " r ", so the radius in this instance is , not 5.

In the course of the to a higher place procedure, about the only other matter that can exist a problem is forgetting the sign on the step where you multiply by one-half. Advisory: If you drop a "minus" sign, you'll get the incorrect answer for the coordinates of the center, then be conscientious of this. Don't try to do this stride in your head: write it out!

---

• Find the center and radius of the circle with the post-obit equation: 100x ² + 100y ² − 100x + 240y − 56 = 0.

This is the equation they've given me:

100x ² + 100y ⁱⁱ − 10010 + 240y − 56 = 0

First, I'll divide through by the coefficient of the squared terms (that is, I'll divide through past 100):

ten ² + y ⁱⁱ − 10 + 2.foury − 0.56 = 0

Second, I'll group with x terms and the y terms together:

x ² − x + y ² + ii.foury − 0.56 = 0

Third, I'll movement the loose numerical term over to the other side of the "equals" sign:

x ² − 10 + y ^two + ii.foury = 0.56

Fourth, I'll rewrite the equation with parentheses around my grouped terms on the left-hand side, leaving space for the squared values that I'll shortly be adding:

(x ² − ten ) + (y ⁱⁱ + ii.4y ) = 0.56

5th, I'll detect half of the coefficients of the linear variable terms. In this case, the coefficient of x is −ane (of which half is −½) and the coefficient of y is +2.four, or +12/five (of which half is +6/v).

Sixth, I'll square each of these values. For the x parentheses, I'll be using the square of −½, which is +¼; for the y parentheses, I'll be using the square of +half-dozen/5, which is +36/25.

Seventh, I'll add these squared terms inside their respective parentheticals on the left-hand side of the equation, and too to the numerical value on the right-hand side of the equation. (For simplicity'southward sake, I'll also convert the decimal form of the numerical value into fractional form. This volition be helpful soon, when I simplify on that side.)

Eighth, I'll rewrite the parentheticals on the left-hand side of the equation in completed-square class:

9th, I'll simplify the numerical stuff on the correct-mitt side of the equation:

Tenth, I'll finish up past finding the value of the radius, which is the square root of the value on the right-hand side of the equation:

Now I have the equation in centre-vertex form, and then I can read the coordinates of the center from the equation; the radius is the square root that I just found. So my answer is:

The animation below shows the tricky part, in the heart, of finding the values for completing the squares and for adding to the correct-hand side:

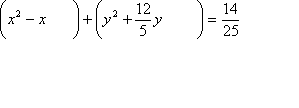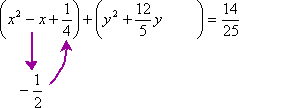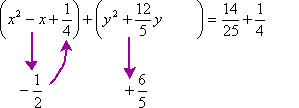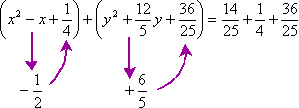
My best communication for you is to practise actress completing-the-square exercises. The steps in the process start to become somewhat automated in one case you've done xx, 30, l of them. Keep practicing until you can consistently and quickly piece of work through the steps to get your answers.

Source: https://www.purplemath.com/modules/sqrcircle.htm

Posted by: williamsuniagard.blogspot.com

Share this post