how to find holes in a graph
HOW TO Observe THE Pigsty OF A RATIONAL FUNCTION
In this section, you will learn how to discover the hole of a rational part
And we will exist able to find the pigsty of a part, only if it is a rational office.
That is, the function has to be in the form of
f(ten) = P/Q
Case : Rational Function
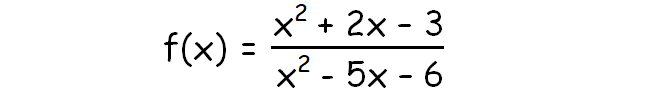
Steps Involved in Finding Pigsty of a Rational Role
Let y = f(x) be the given rational function.
Step one :
If it is possible, factor the polynomials which are found at the numerator and denominator.
Step 2 :
After having factored the polynomials at the numerator and denominator, we have to run into, whether there is whatever mutual cistron at both numerator and denominator.
Instance 1 :
If there is no common factor at both numerator and denominator, at that place is no hole for the rational function.
Case two :
If in that location is a common gene at both numerator and denominator, there is a hole for the rational function.
Step 3 :
Let (10 - a) be the common factor constitute at both numerator and denominator.
Now nosotros have to make (x - a) equal to zip.
When nosotros do so, we become
x - a = 0
ten = a
And so, at that place is a hole atten = a.
Step iv :
Let y = b for 10 = a.
And so, the hole volition announced on the graph at the point (a, b).
Examples
Example ane :
Find the hole (if whatever) of the function given beneath
f(10) = one / (x + six)
Solution :
Pace 1:
In the given rational function, clearly in that location is no common gene found at both numerator and denominator.
Step two :
Then, there is no hole for the given rational part.
Example 2 :
Find the hole (if any) of the role given below.
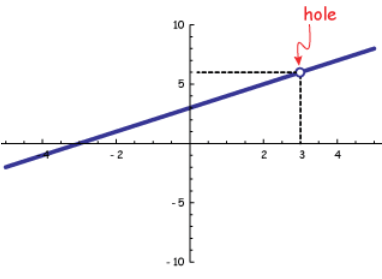
f(ten) = (xii+ 2x - 3) / (102- 5x + half dozen)
Solution :
Step 1:
In the given rational function, let us cistron the numerator and denominator.
f(ten) = [(10 + iii)(x - 1)] / [(ten - 2)(x - iii)]
Step 2 :
After having factored, there is no common factor establish at both numerator and denominator.
Step three :
Hence, there is no hole for the given rational function.
Instance 3 :
Find the pigsty (if whatsoever) of the function given below.
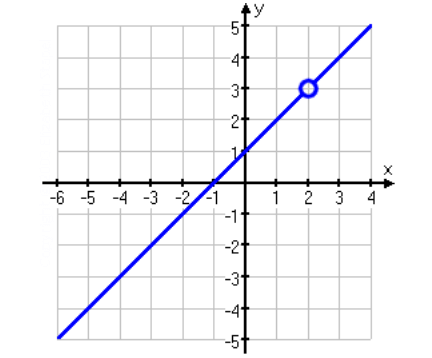
f(x) = (x2 - 10 - 2) / (x - 2)
Solution :
Step 1:
In the given rational function, let us gene the numerator .
f(x) = [(x-ii)(10+1)] / (x-2)
Footstep two :
Afterwards having factored, the common factor found at both numerator and denominator is (x - 2).
Step iii :
At present, we take to make this common factor (ten-two) equal to zero.
10 - 2 = 0
10 = two
So, there is a hole at
x = 2
Stride 4 :
After crossing out the common factors at both numerator and denominator in the given rational function, we get
f(10) = ten + ane ------(1)
If nosotros substitute 2 for x, we become go
f(2) = 3
And then, the hole will appear on the graph at the point (2, 3) .

Autonomously from the stuff given in this section, if you need any other stuff in math, please utilize our google custom search here.
Kindly post your feedback tov4formath@gmail.com
We always appreciate your feedback.
Give-and-take Bug
HCF and LCM discussion problems
Give-and-take bug on simple equations
Word bug on linear equations
Word problems on quadratic equations
Algebra word problems
Word problems on trains
Area and perimeter word issues
Word issues on directly variation and changed variation
Word problems on unit price
Discussion problems on unit rate
Give-and-take bug on comparing rates
Converting customary units discussion bug
Converting metric units word problems
Word problems on simple involvement
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word issues
Double facts give-and-take problems
Trigonometry word problems
Percentage word bug
Profit and loss word problems
Markup and markdown word bug
Decimal word bug
Word problems on fractions
Discussion problems on mixed fractions
One footstep equation discussion issues
Linear inequalities word problems
Ratio and proportion word bug
Time and work give-and-take bug
Word problems on sets and Venn diagrams
Word problems on ages
Pythagorean theorem give-and-take problems
Per centum of a number word problems
Word problems on constant speed
Word problems on boilerplate speed
Give-and-take bug on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Profit and loss shortcuts
Percent shortcuts
Times table shortcuts
Fourth dimension, speed and altitude shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long sectionalization
L.C.Thou method to solve time and work problems
Translating the discussion problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by vii
Sum of all three digit numbers divisible by 8
Sum of all 3 digit numbers formed using ane, 3, four
Sum of all three 4 digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all iii four digit numbers formed using 1, 2, five, 6
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/how-to-find-the-hole-of-a-rational-function.html
Posted by: williamsuniagard.blogspot.com

0 Response to "how to find holes in a graph"
Post a Comment